Dice of the Royal Game of Ur
In the Royal Game of Ur, even if you are losing, a few lucky rolls at the right time could win you the game! This page goes through the different types of dice used in the game, and the probabilities of rolling the values you need.

Table of Contents
Tetrahedral Dice
The most commonly used dice when playing the Royal Game of Ur are the tetrahedral dice, which are dice that are shaped like triangle-based pyramids. These dice are difficult to pick up and roll, but despite this, they are strongly associated with the Royal Game of Ur. This is because sir Leonard Woolley excavated a set of these unique tetrahedral dice alongside the RGU game boards that were dated to 2600 BCE (over 4500 years ago!).
How do they work? Each die has two corners marked with white, and two unmarked corners. After rolling the dice, you can count the number of die with a marked corner facing upwards to get your roll!
Throwing Stick Dice
Throwing sticks are another type of dice that are commonly used to play The Royal Game of Ur. Throwing stick dice are two-sided sticks with one side marked. They are commonly used in other ancient games that are similar to the Royal Game of Ur, such as Aseb or Senet. Aseb is actually so similar to the Royal Game of Ur that they both share another name, "the Game of 20 Squares".
How do they work? The dice can be held as a bunch to be rolled. The number that was rolled can then be found by counting the number of sticks with their marked sides facing upwards.

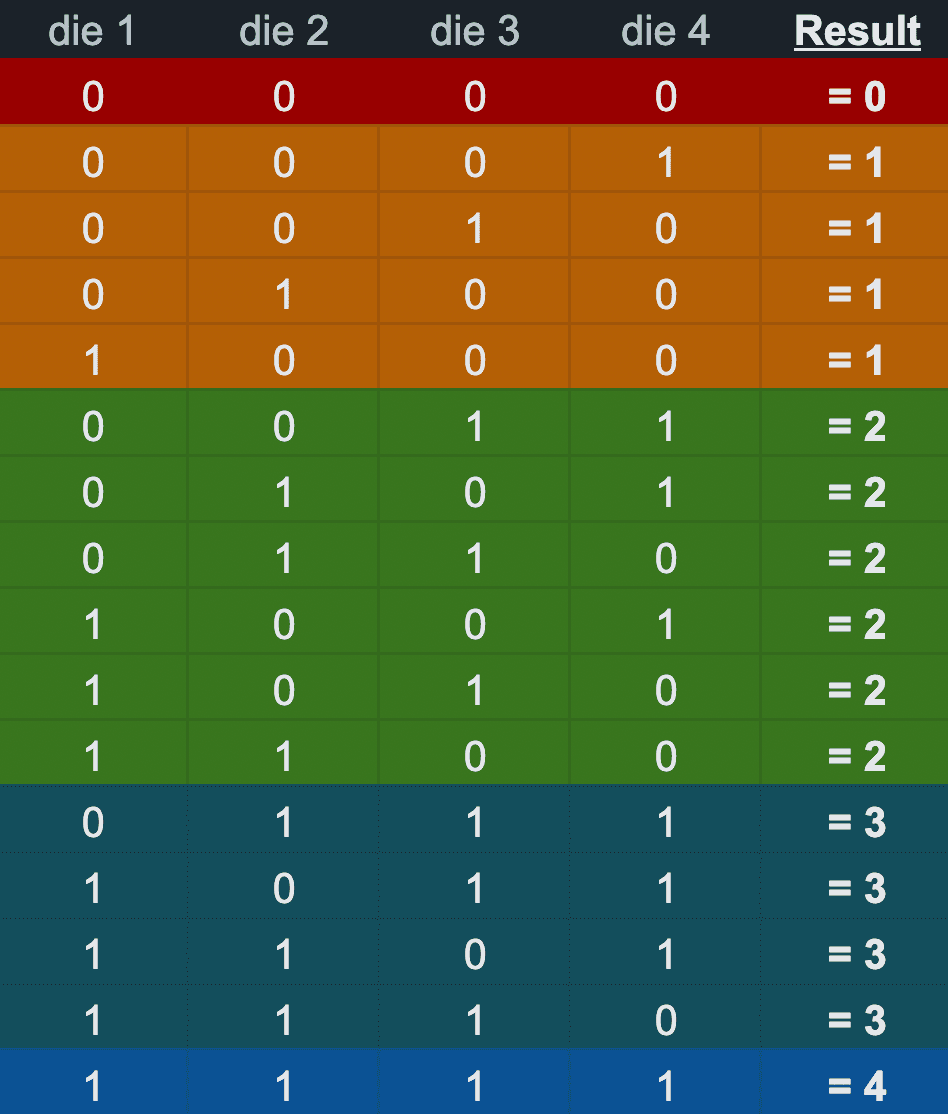
Knucklebone Dice (Astragals)
A cuneiform tablet deciphered by Irving Finkel described some more complicated rules for playing the Royal Game of Ur. These rules instructed players to use two astragals (that is, knucklebones) for dice. The tablet called for one sheep astragal, and one ox astragal. Sheep astragal were commonly used for dice, as they are easy to roll. However, ox astragal are very unusual to use as dice, as they are much larger than sheep astragal. This has led to different theories about how the two astragals were to be used together to play the game.
How do they work? Typically, four of the sides of the knucklebone dice are given different values, as shown in the figure below. When you roll them, you can then identify the upwards facing side, and use that to get the value of your roll.
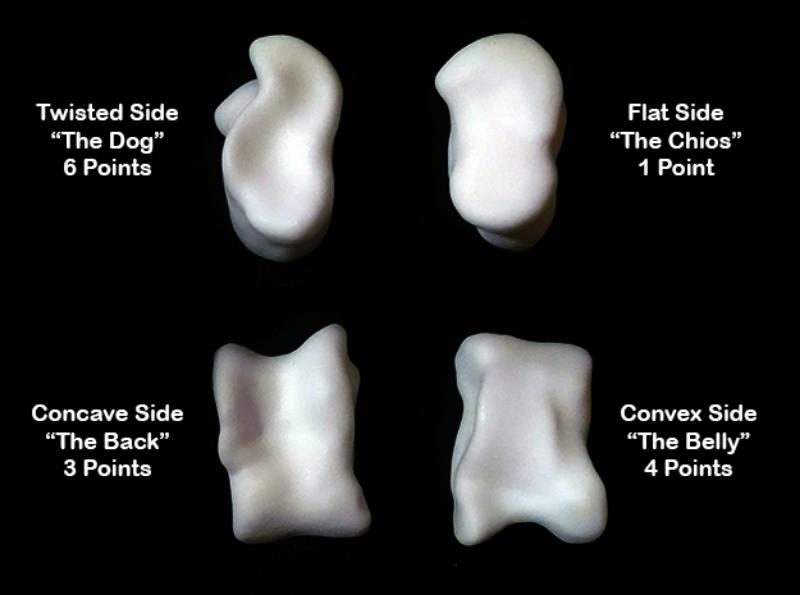
Probability of rolls
Both the tetrahedral dice and the stick dice discussed above are examples of binary dice. This means that each die in this set has two possible outcomes: either they land with a marked side facing up, or they don't. There is a 50/50 chance of each of these outcomes after rolling each die. The number of die with a marked face upwards can then be counted to get the final value of a roll. This leads to predictable likelihoods of rolling a 0, 1, 2, 3, or 4 when you roll!
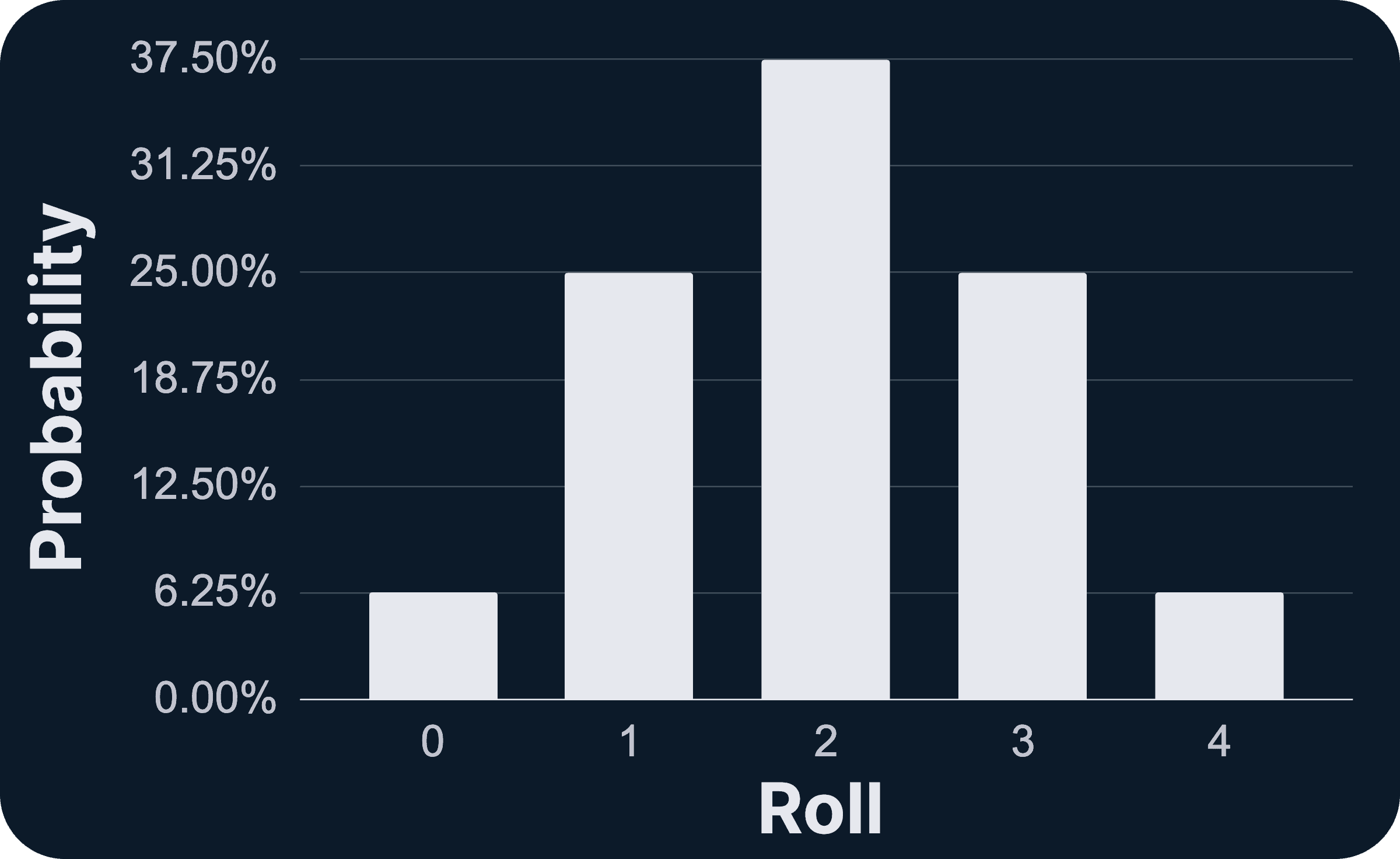
Using three dice instead of four
There are also many people who use three dice instead of four, as many consider this to be more historically accurate. When using three dice, most people treat a roll of zero as allowing you to move four tiles, instead of skipping your turn.
It turns out, when you use three dice like this instead of four dice, the probably distribution changes quite a bit! Rolling either one or two now both have the same probability of 37.5%. Similarly, rolling either three or four also have the same probability of 12.5%.
Calculating the probabilities
We can calculate the probabilities of rolling each value using dice by counting all the different dice rolls we could make. When using four dice, there are only 16 possible outcomes when rolling four tetrahedral or stick dice.
For example, rolling a zero can only happen in one specific way: all dice being zero, or 0000. In contrast, rolling a one can occur in four different ways: 1000, 0100, 0010, or 0001. Any of the four die could have its marked side up. This leads to a 1 in 16 chance (or 6.25%) of rolling a zero, but a 4 in 16 chance (25%) of rolling a one! This is what leads to the imbalance in the probability of rolling each number.